Redefining Household Sampling: A GIS-Based Approach Using OpenStreetMap and Python
Have you ever found yourself staring at a blank map, wondering how to select the right households for your research? Field researchers often face this challenge, especially when a reliable sampling frame is scarce. One common workaround is a crude method where enumerators would spin a bottle to determine a walking direction and then select households at regular intervals along the way. While this method may seem practical, it is far from precise. Selection bias from enumerators and challenges in maintaining consistent intervals can compromise the reliability of the sample.
This is where the untapped potential of OpenStreetMap (OSM) becomes invaluable. With its detailed maps and open-access data, OSM offers a treasure trove of information that can be leveraged for research. What if you could use OSM to extract building footprints and residential areas, and then employ GIS tools to create a representative sample? Even without a formal household list, this approach can provide an efficient alternative. This blog post will provide you with insight into GIS-based sampling using OSM and Python. We will extract GIS data from OSM, perform spatial operations, and employ Probability Proportional to Household Size (PPS) sampling to generate a representative sample of households. Even if you are not a GIS expert or a Python whiz, this post will help you apply these tools to your context. Let’s dive in, and load the essential Python libraries. If you have not already done so, you will need to install these libraries from your command prompt using pip or conda depending upon your Python environment.
import osmnx as ox # Fetches map data from OpenStreetMap.
import geopandas as gpd # Handles geospatial data (maps, points, polygons).
import pandas as pd # Data management and analysis.
import numpy as np # For numerical computations.
from shapely.geometry import Point # For geometric operations on shapes.
import matplotlib.pyplot as plt # Data visualisation.
from matplotlib.patches import Rectangle # Draw shapes on plots.
from matplotlib_scalebar.scalebar import ScaleBar # Add scale bars to maps.
from geo_northarrow import add_north_arrow # Add north arrows to maps.Extracting GIS Data with OSM
In this blog, we consider Ward Number 5 of Sunkoshi Village in Bagmati Province, Nepal as our study site. Using the osmnx Python library, we first extract the geographic extent of our study area. Subsequently, we extract all building footprints within this defined boundary. OSM data is tagged with specific keywords to categorize map elements. For instance, the building=yes tag identifies structures. However, these tags can vary in detail. While some buildings are labelled as building=house or building=apartment, others are simply labelled as building=yes. You can find more information about OSM tags on OpenStreetMap TagInfo.
In our study site, building footprints lack specific labels, making it difficult to distinguish between residential and non-residential structures. To address this ambiguity, we extract all buildings along with their enclosing areas, such as residential zones, schools, and parks. Later, during the cleaning process, we will specifically focus on the landuse=residential tag to refine the dataset. This approach ensures that buildings located in non-residential areas are excluded, leaving a dataset that is more likely to represent households.
# Get the boundary of the study village
ward = "Sunkoshi-05, Sindhuli, Bagmati, Province, Nepal"
boundary = ox.geocoder.geocode_to_gdf(ward)
# Collect all building footprints
tags_buildings = {"building": True}
try:
buildings = ox.features_from_polygon(boundary.geometry.iloc[0], tags_buildings)
print(f"Retrieved {len(buildings)} building features.")
except Exception as e:
print(f"Error fetching buildings: {e}")
exit()
# Collect all potential enclosing areas (hamlets)
tags_hamlet = {"landuse": ["residential"], "amenity": True, "boundary": True}
try:
hamlet = ox.features_from_polygon(boundary.geometry.iloc[0], tags_hamlet)
print(f"Retrieved {len(hamlet)} hamlet features.")
except Exception as e:
print(f"Error fetching hamlets: {e}")
exit()Data Preparation
So far, we have extracted all building footprints from our study site and stored them in the buildings dataset. The enclosing boundaries are stored in the hamlet dataset. We project both datasets to UTM Zone 45N (EPSG:32645) to obtain the geo-points of each building and the area of each enclosing boundary. We then use the sjoin function from the geopandas library to link buildings to their corresponding enclosing areas. This creates a new DataFrame called hhlist. After cleaning the hhlist dataset to remove non-residential boundaries and enclosed buildings, we are left with 1264 buildings enclosed within 80 residential areas. We refer to these buildings as households and residential areas as hamlets. (known locally as toles). Each household is our sampling unit, and hamlets are our enumeration areas.
# Re-project both datasets to a projected CRS for spatial operations
buildings = buildings.to_crs(epsg=32645)
hamlet = hamlet.to_crs(epsg=32645)
# Extract X, Y coordinates of households and calculate hamlet areas
buildings['centroid'] = buildings.geometry.centroid
buildings['centroid'] = buildings['centroid'].to_crs(epsg=4326)
buildings['longitude'] = buildings['centroid'].x
buildings['latitude'] = buildings['centroid'].y
hamlet['area'] = hamlet.geometry.area
# Assign each household to its immediate hamlet using a spatial join
hhlist = gpd.sjoin(
buildings,
hamlet,
how="left",
predicate="within"
)
# Clean the Datasets
hhlist.dropna(subset=['landuse'], inplace=True) # Remove households without hamlet assignment
hhlist = hhlist.dropna(axis=1, how='all') # Drop columns with all NaN values
hhlist.reset_index(inplace=True)
hhlist = hhlist.drop(
columns=['element_type_left', 'nodes_left', 'building', 'geometry', 'centroid',
'element_type_right', 'nodes_right', 'landuse', 'source']
)
hhlist.rename(columns={'osmid_left': 'hh_id', 'osmid_right': 'hamlet_id'}, inplace=True)
hamlet.dropna(subset=['landuse'], inplace=True)
hamlet = hamlet.dropna(axis=1, how='all')
hamlet.reset_index(inplace=True)
hamlet = hamlet.drop(columns=['element_type', 'landuse', 'nodes'])
hamlet.rename(columns={'osmid': 'hamlet_id'}, inplace=True)Sample Allocation
From now on, we will work on the hhlist dataset to sample 200 households across the study area using PPS sampling. We aim to select households from each hamlet proportionally to its estimated household size. However, the number of households derived from OSM data may not precisely match the actual household count, such as that reported in a census. For instance, some buildings might represent non-residential structures or be mislabelled in the OSM dataset. We adjust this discrepancy by calculating an adjustment factor based on the ratio of the census-reported total households to the number of households derived from OSM. This adjustment factor is then applied to estimate the adjusted household count (adj_hh) and the expected sample size (hh_size) for each hamlet.
We allocate the total sample proportionally, ensuring that denser hamlets receive larger samples while sparser hamlets receive smaller ones. Some hamlets are extremely sparse, with as few as two households, which could lead to null representation. So, we assign a minimum sample size of 1 to these sparsest hamlets. This truncation process can sometimes result in a surplus in the total sample size. In our case, we have a surplus of four households. We redistribute the surplus by reducing the sample size by 1 unit from the four densest hamlets. Once the sample size for each hamlet is determined, we randomly select households within each hamlet. This approach balances precision and inclusivity, but it is important to consider the implications of these decisions. For example, what if we did not impose a minimum sample size? How would the sample allocation and adjustment process change if the total sample size were smaller? What if we used systematic selection instead of random selection? Take a moment to think about these scenarios—how would they impact the representativeness and feasibility of your sampling strategy?
# Calculate household density
hhlist['hh_size'] = hhlist.groupby('hamlet_id')['hh_id'].transform('count')
hhlist['density'] = hhlist['hh_size'] / hhlist['area']
# Calculate the adjustment factor and adjusted household size
census_total = 1152
osm_total = len(hhlist)
afactor = census_total / osm_total
hhlist['adj_hh'] = (hhlist['hh_size'] * afactor).round().astype(int)
# Allocate sample sizes using PPS
total_sample = 200
hhlist['sample_size'] = (hhlist['adj_hh'] / census_total * total_sample).round().astype(int)
# Ensure a minimum sample size of 1 for hamlets with null samples
hhlist.loc[hhlist['sample_size'] == 0, 'sample_size'] = 1
# Adjust sample sizes for densest hamlets
sample_adjustment = total_sample - hhlist.groupby('hamlet_id')['sample_size'].first().sum()
if sample_adjustment != 0:
# Get indices of the densest hamlets
dense_areas = hhlist.sort_values(
'density', ascending=False)['hamlet_id'].unique()[:abs(sample_adjustment)]
# Adjust sample size for each selected hamlets
for hamlet_id in dense_areas:
area_adjustment = np.sign(sample_adjustment)
# Update sample size for all households in the hanlet
hhlist.loc[hhlist['hamlet_id'] == hamlet_id, 'sample_size'] += area_adjustmentEach sampled household is represented by its XY coordinates, which are included in the hhsample dataset. Enumerators can use these coordinates as a reference to locate households during fieldwork. It is important to note that the XY coordinates may not always perfectly align with a specific household structure in reality, due to discrepancies in OSM data or the spatial resolution of GPS devices. In such cases, enumerators should select the nearest household to the indicated point. This ensures practical feasibility while maintaining the integrity of the sampling strategy.
# Create an empty list to store sampled rows
sampled_rows = []
# Group by hamlets
grouped = hhlist.groupby('hamlet_id')
for hamlet_id, group in grouped:
# Get the sample size for the current hamlet
sample_size = group['sample_size'].iloc[0]
# Randomly select the required number of households
sampled_rows.append(group.sample(n=sample_size, random_state=42))
# Concatenate all sampled households into a single DataFrame
hhsample = pd.concat(sampled_rows)
hhsample = hhsample.reset_index(drop=True)Data Visualisation
The final output is a map showcasing the sampled households, distributed proportionally across the hamlets in the study area. Here, we use the matplotlib Python library and its related dependencies to visualise the village boundary, hamlets and sampled households within them. The output is then saved as a high-resolution TIFF file for further use.
# Prepare the dataset containing sampled households for visualisation
hhsample['geometry'] = [Point(xy) for xy in zip(hhsample['longitude'], hhsample['latitude'])]
hhsample = gpd.GeoDataFrame(hhsample, geometry='geometry')
hhsample.crs = "EPSG:4326"
hhsample = hhsample.to_crs(epsg=32645)
boundary = boundary.to_crs(epsg=32645)
# Plot
fig, ax = plt.subplots(figsize=(10, 10))
boundary.plot(ax=ax, facecolor='none', edgecolor='black', linewidth=1)
hamlet.plot(ax=ax, facecolor='#e8e8e8', edgecolor='#e8e8e8', linewidth=0)
hhsample.plot(ax=ax, color='#b3005a', markersize=2.5, marker = ".", alpha=1)
# Add legend
legend_elements = [
Rectangle((0, 0), 1, 1, linewidth=1, edgecolor='black', facecolor='none', label='Village'),
Rectangle((0, 0), 1, 1, linewidth=0, edgecolor='#e8e8e8', facecolor='#e8e8e8', label='Hamlet'),
plt.Line2D([0], [0], color='#b3005a', lw=0, marker='.', markersize=7.5, label='Sample HH')
]
ax.legend(handles=legend_elements, loc='lower left', fontsize=12, frameon=False, ncol=1)
# Add scalebar and north arrow
scalebar = ScaleBar(dx=1, units='m', dimension="si-length", length_fraction=0.125,
location='lower right', frameon=False)
ax.add_artist(scalebar)
add_north_arrow(ax, scale=.3, xlim_pos=.9, ylim_pos=.9, color='#000', text_scaler=4, text_yT=-2)
# Set plot aesthetics and export map
ax.set_axis_off()
plt.tight_layout()
plt.savefig("sample_village.tiff", dpi=300, bbox_inches='tight')
plt.show()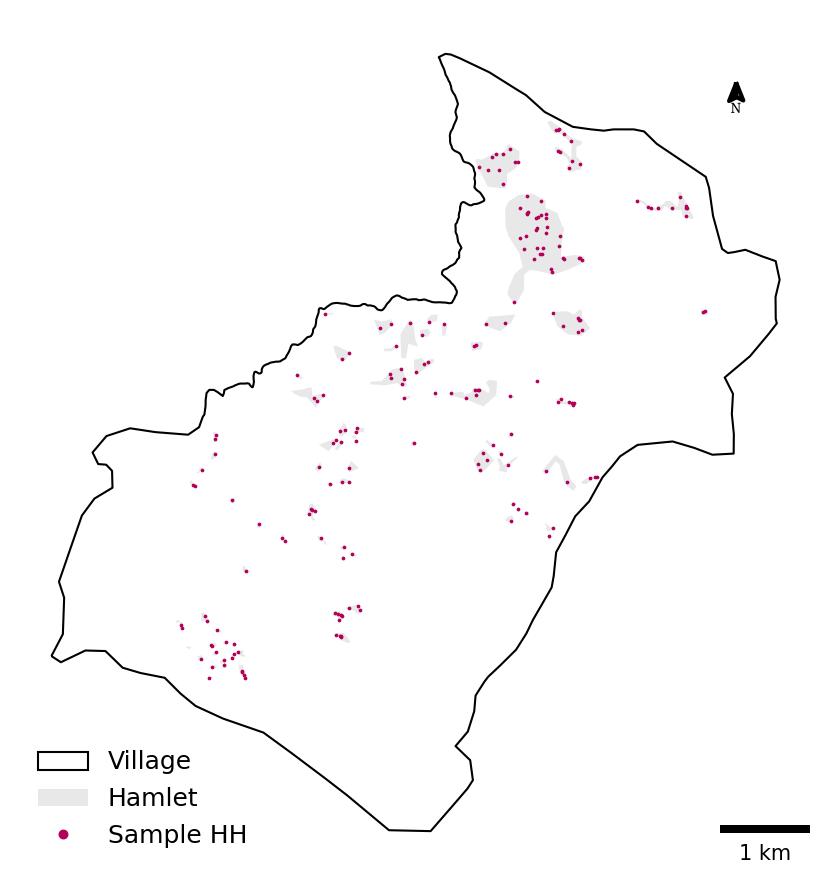
We prepare the sampled household data for export by dropping unnecessary columns and retaining only the essential identifiers and coordinates. Direct export of a GeoDataFrame can sometimes cause issues with geometry columns. We convert it to a regular panda DataFrame to ensure compatibility and save it as a CSV file.
# Save the File Containing Sampled Household
hhsample = hhsample.drop(columns=['area', 'hh_size', 'density', 'adj_hh', 'sample_size', 'geometry'])
hhsample = hhsample[['hh_id', 'hamlet_id', 'longitude', 'latitude']]
hhsample.to_csv('hhsample.csv', index=False)Concluding Remarks
This blog post demonstrated how GIS-based sampling using OSM and Python can provide a systematic alternative to traditional household selection methods, even without formal sampling frames. While OSM data offers valuable open-access data, its inconsistencies—such as incomplete or ambiguous building tags— may require some level of field validation to ensure the accuracy of the sampled geo-coordinates. Moreover, the precision of the generated coordinates may vary, requiring adjustments by enumerators during fieldwork. Despite these limitations, GIS-based sampling remains a flexible and adaptable approach. By tailoring these methods to specific research contexts, researchers can create transparent and efficient sampling strategies. As you consider implementing this approach, think critically about how the quality of OSM data in your study area might influence your sample size and overall feasibility.
